Возведение числа в степень, извлечение корня
Калькулятор степеней и извлечения корня
Для возведения числа в степень и нахождения корня, введите число и степень.
Возведение в положительную и отрицательную степень
Положительная степень
Степень числа a с натуральным показателем n (n>1) можно представить в виде произведения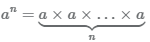 
Пример Выполнить возведение в степень.
Выполним возведение в степень положительных и отрицательных чисел, десятичных дробей, правильных и смешанных дробей.
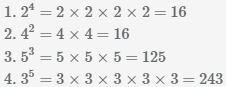
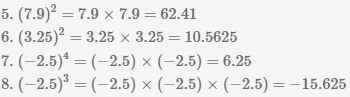
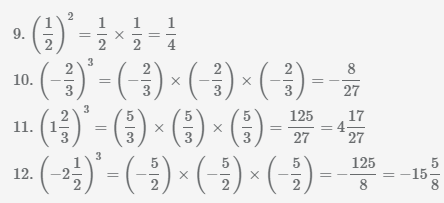
Отрицательная степень
Степень числа a с отрицательным натуральным показателем n (n<1) можно представить в виде произведения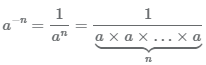 
Числа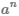 
и 
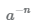являются взаимно обратными и их произведение равно единице 
.
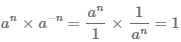Пример Вычислить значение числа в отрицательной степени.
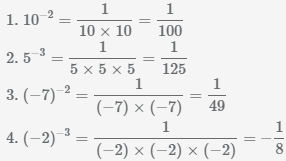
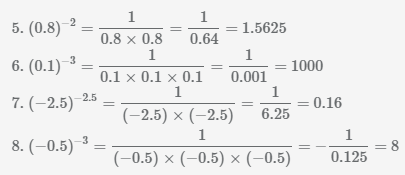
Пример Выполните возведение дроби в отрицательную степень.
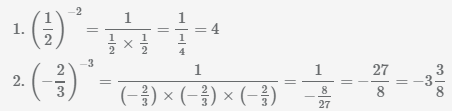
Иногда значительно легче вычислить дробь в отрицательной степени, сразу поменяв числить и знаменатель местами и умножив степень на -1. Рассмотрим данное преобразования на примерах.
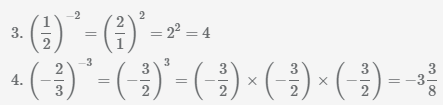
Корень из числа
Корень нечётной степени из положительного числа
В результате вычисления корня нечётной степени из положительного числа будет положительное число: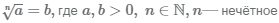 
.
Пример Вычислим корни нечётной степени из 8, 27, 125, 243
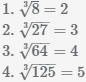
Корни 3 степени также называют кубическими корнями.
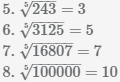
В результате вычисления корней 5-ой степени из положительных чисел, получили также положительные числа.
Корень нечётной степени из отрицательного числа
В результате вычисления корня нечётной степени из отрицательного числа будет отрицательное число: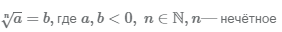 
.
Пример Найдем корни 3 и 5 степеней из отрицательных чисел.
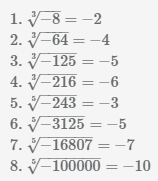
Корень четной степени из положительного числа
Корень чётной степени из положительного числа имеет два значения, положительное и отрицательное: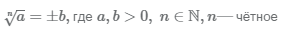 
.
Пример Вычислим корни 2 и 4 степени.
Корень 2-й степени называют квадратный корнем.
Корень четной степени из отрицательного числа
Корень четной степени из отрицательного числа не существует для вещественных чисел.
Корень любой степени из нуля
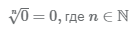
Числа в степени -1, 0, 1
Число в -1 степени
Число 3 в -1 степени можно представить в виде дроби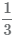 
.Обратная операция также верна 
,
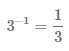любую дробь можно представить как число в -1 степени, для этого нужно поменять числить и знаменатель местами.
Число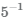 
является обратным числом 5, т.е. их произведение равно единице 
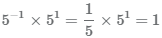, такое равенство выполнено для любого числа
Пример Представить дробь в степени -1
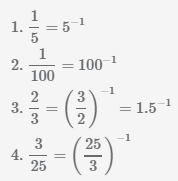
Число в 1 степени
Число в первой степени является самим числом a1=a
Число в 0 степени
Любое число в степени ноль равно единице a0=1