Bruchrechner
Online Bruchrechner
Brüche addieren und subtrahieren
Brüche werden addiert/subdrahiert indem man sie gleichnamig macht, dass heißt auf den gleichen Nenner erweitert und dann die Zähler addiert/subdrahiert und den gemeinsamen Nenner beibehält
Beispiel Addition von Brüchen 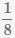 +
+ 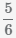
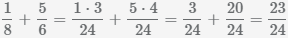 .
.
Kleinste gemeinsame Vielfache (kgV) der Nenner kgv(8, 6)=24.
Praktisches Rechnen mit Brüchen. Die Brüche, die addiert oder subtrahiert werden sollen, werden zunächst gleichnamig gemacht, anschließend werden ihre Zähler addiert bzw. subtrahiert.
Beispiel Subtraktion von Brüchen 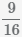 und
und 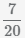
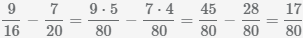 .
.
Kleinste gemeinsame Vielfache der Nenner kgv(16, 20)=80.
Brüche multiplizieren und dividieren
Brüche werden miteinander multipliziert indem man jeweils die Zähler und die Nenner miteinander multipliziert.
Beim Multiplizieren von Bruchtermen müssen sowohl die Zähler als auch die Nenner multipliziert werden. Gemeinsame Faktoren von Zähler und Nenner sollten herausgekürzt werden.
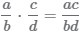 .
.
Beispiel Multiplikation von Brüchen 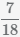 und
und 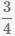
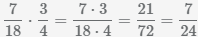 .
.
Durch einen Bruch wird dividiert indem man mit der Kehrzahl multipliziert. Die Kehrzahl eines Bruches erhält man indem man den Zähler mit dem Nenner vertauscht.Die Division von Bruchtermen lässt sich auf die Multiplikation zurückführen. Man dividiert durch einen Bruchterm, indem man mit seinem Kehrwert multipliziert.
Beispiel Division von Brüchen  und
und 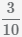
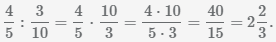 .
.
Merke
Der Wert der durch einen Bruch dargestellten Bruchzahl ändert sich nicht, wenn man Zähler und Nenner des Bruches mit derselben Zahl multipliziert (den Bruch erweitert) oder durch einen gemeinsamen Teiler von Zähler und Nenner teilt (den Bruch kürzt).