Теорема синусов
Теорема синусов
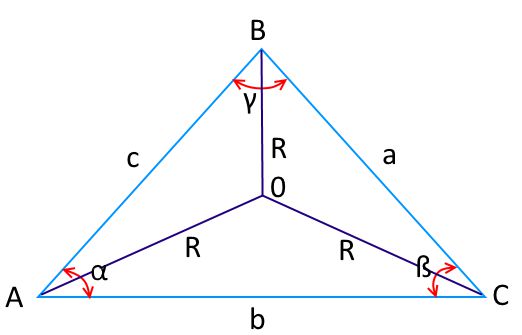
\begin{align} & \text{Во всяком треугольнике отношение любой стороны к синусу противолежащего ей угла}\\ & \text{постоянно и равно диаметру описанной вокруг треугольника окружности.}\\ & \frac{a}{\sin{\alpha}}=\frac{b}{\sin{\beta}}=\frac{c}{\sin{\gamma}}=2R\\ & \angle{BAC}=\alpha,\ \angle{ABC}=\beta,\ \angle{ACB}=\gamma,\ R-радиус\ описанной\ окружности\\ \end{align}
Пример 1
\begin{align} & \text{Даны сторона a=16, угол } \alpha = 60°, \text{ сторона b=8, найти угол } \beta. \\ & \text{Воспользуемся теоремой синусов, получим } \frac{a}{\sin{\alpha}} = \frac{b}{\sin{\beta}}\\ & \text{подставим заданные значения } \frac{16}{\sin{60°}} = \frac{8}{\sin{\beta}}\\ & sin{\beta} = \frac{8\sin{60°}}{16}=\frac{8\sqrt{3}}{16 * 2}==\frac{\sqrt{3}}{4}\\ & \beta \approx 25.66 \\ \end{align}
Даны сторона a, угол α, противолежащий стороне, сторона b.
Найти значение противолежащего стороне b угла β.
Пример 2
\begin{align} & \text{Даны сторона a=16, угол } \alpha = 60°, \text{ угол } \beta=45° \text{, найти сторону b } \\ & \text{Воспользуемся теоремой синусов, получим } \frac{a}{\sin{\alpha}} = \frac{b}{\sin{\beta}}\\ & \text{подставим заданные значения } \frac{16}{\sin{60°}} = \frac{b}{\sin{45°}}\\ & b = \frac{16 sin{45°}}{sin{60°}}=\frac{16\sqrt{2}}{\sqrt{3}}\\ & b \approx 13.06 \\ \end{align}
Даны сторона a, угол α, противолежащий стороне, угол β.
Найти значение стороне b, противолежащей углу β.
Пример 2
\begin{align} & \text{Даны сторона a=16, угол } \alpha = 60°. \text{ Найти радиус описанной окружности R } \\ & \text{Воспользуемся теоремой синусов, получим } \frac{a}{\sin{\alpha}} =2R\\ & \text{подставим заданные значения } \frac{16}{\sin{60°}} = 2R\\ & R = \frac{8}{sin{60°}}=\frac{16}{\sqrt{3}}\\ & b \approx 18.47 \\ \end{align}