Теорема косинусов
Теорема косинусов
\begin{align} & \text{Во всяком треугольнике квадрат одной из сторон равен сумме квадратов двух других}\\ & \text{сторон минус удвоенное произведение этих сторон на косинус угла,}\\ & \text{заключенного между ними}\\ & c^2=a^2+b^2-2ab \cos{\beta}\\ \end{align}
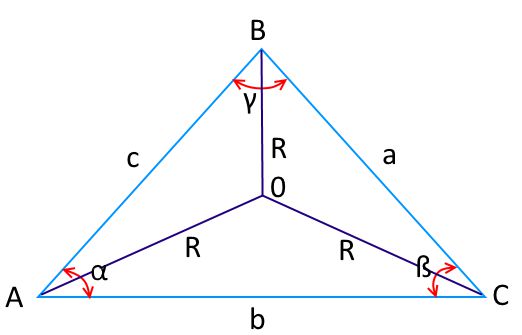
Применение теоремы косинусов
- Для нахождения стороны, когда известны 2 стороны и угол между ними.
- Для нахождения угла, когда известные 3 стороны.
Пример 1
\begin{align} & \text{Даны сторона a=10, сторона b=8, угол между ними β=60°. Найти сторону c.}\\ & \text{Воспользуемся теоремой косинусов, получим } c^2=a^2+b^2-2ab \cos{\beta}\\ & \text{подставим заданные значения } c^2=10^2+8^2-2*10 * 8 \cos{60°}\\ & c=2\sqrt{21}\\ & c \approx 9.16\\ \end{align}
Даны сторона a, сторона b, угол между β.
Найти значение стороны c.
Пример 2
\begin{align} & \text{Даны стороны a=16, b=10, c=13. Найти углы } \alpha,\ \beta,\ \gamma . \\ & \text{Воспользуемся теоремой косинусов, найдем } \alpha : \\ & \ \ a^2=c^2+b^2-2cb \cos{\alpha}\\ & \ \ 16^2=13^2+10^2-2 * 13 * 10 \cos{\alpha}\\ & \ \ \cos{\alpha} = \frac{1}{20}\\ & \ \ \alpha \approx 87.13°,\\ \\ & найдем\ \beta:\\ & \ \ c^2=a^2+b^2-2ab \cos{\beta}\\ & \ \ 13^2=16^2+10^2-2 * 16 * 10 \cos{\beta}\\ & \ \ \cos{\beta} = \frac{187}{320}\\ & \ \ \beta \approx 54.24 °,\\ \\ & найдем\ \gamma:\\ & \ \ b^2=a^2+c^2-2ac \cos{\gamma}\\ & \ \ 10^2=16^2+13^2-2 * 16 * 13 \cos{\gamma}\\ & \ \ \cos{\gamma} = \frac{325}{416}\\ & \ \ \gamma \approx 38.62°.\\ \end{align}