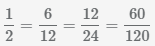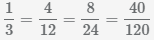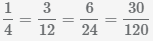Наименьший общий знаменатель
Общий знаменатель
Общий знаменатель
Знаменатель дроби показывает на сколько частей разделили целое  .
.
Числитель и знаменатель дроби 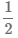 можно умножить на одно и то же число 3,
в результате получится равная дробь
можно умножить на одно и то же число 3,
в результате получится равная дробь 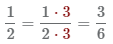 .
.
Дроби 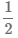 ,
, 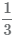 и
и 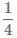 можно привести к одинаковым знаменателям, также называемым общим знаменателем.
можно привести к одинаковым знаменателям, также называемым общим знаменателем.
1/2
1/3
1/4
Пример Дроби  ,
, 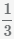 и
и 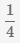 приведены к одинаковым знаменателям
приведены к одинаковым знаменателям
Дроби с разными знаменателями сложение, вычитание, сравнение
Сложение и вычитание дробей с разными знаменателями.
Часто возникает ситуация когда необходимо сложить две дроби с разными знаменателями Вы можете легко складывать дроби с одинаковыми знаменателями, а как поступить в ситуации если знаменатели дробей различны? Для сложения дробей с разными знаменателями нужно привести дроби к одному знаменателю а затем сложить их числители.
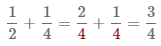
1/2

1/4

3/4
Для сложения, вычитания, сравнения дробей с разными знаменателями, дроби нужно привести к общему знаменателю.
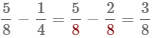
5/8

1/4

3/8
Нахождения общего знаменателя
Простой способ нахождения общего знаменателя - перемножить знаменатели между собой. Рассмотрим данный способ на примере.
Пример Найти разность дробей 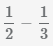 .
.

Наименьший общий знаменатель
Наименьший общий знаменатель
Общий знаменатель дробей 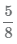 и
и 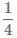 получаемый с помощью умножения достаточно велик 8 × 4 = 24, что усложнит дальнейшее преобразование дробей, попробуем найти общий знаменатель меньше 24.
получаемый с помощью умножения достаточно велик 8 × 4 = 24, что усложнит дальнейшее преобразование дробей, попробуем найти общий знаменатель меньше 24.
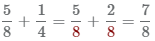
5/8

1/4

7/8
Запишем результат умножения знаменателей на натуральные числа:
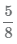 : 8, 16, 24, 32, 40, 48, ...
: 8, 16, 24, 32, 40, 48, ...
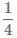 : 4, 8, 12, 16, 20, 24, ...
: 4, 8, 12, 16, 20, 24, ...
Выберем наименьшее общее число:
кратные 8 : 8, 16 , 24 , 32 , 40 , 48 , ...
кратные 4 : 4 , 8, 12 , 16 , 20 , 24 , ...
Число 8 является наименьшим общим знаменателем дробей
Приведем дроби к данному знаменателю, для этого сделаем:
- Дробь
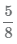 останется не изменной, 8 ÷ 8 = 1.
останется не изменной, 8 ÷ 8 = 1. - Числитель и знаменатель дроби
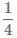 нужно умножить на 8 ÷ 4 = 2, получим дробь
нужно умножить на 8 ÷ 4 = 2, получим дробь 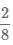
Полученные дроби легко сложить 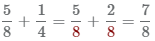 .
После сложений дробей, нужно проверить можно ли сократить дробь, в данном примере числитель и знаменатель взаимно простые число, т.е. их нельзя сократить.
.
После сложений дробей, нужно проверить можно ли сократить дробь, в данном примере числитель и знаменатель взаимно простые число, т.е. их нельзя сократить.
Нахождения наименьшего общего знаменателя
Распишем поэтапно как найти наименьший общий знаменатель дробей 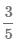 и
и 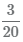 , чтобы сложить дроби.
, чтобы сложить дроби.
- 1 Найти наименьшее общее кратное знаменателей дробей, НОК(5, 20)=20.
-
2 Умножать числить и знаменатель первой дроби на НОК(5, 20) ÷ 5=4, в результате получим дробь
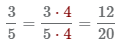 .
.
- 3 Знаменатель второй дроби равен НОК(5, 20), дробь преобразовывать не нужно.
-
4 Сложим полученные дроби
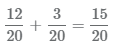 , получим дробь которую можно сократить
, получим дробь которую можно сократить 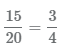 .
.
Преобразования 1-4 можно записать в виде выражения 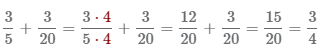 .
.
Пример Найти сумму дробей 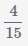 и
и 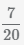 с разными знаменателями.
с разными знаменателями.
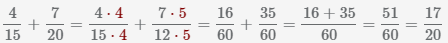
Наименьший общий знаменатель дробей равен НОК(15, 12)=60.
Сократим дробь 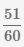 , разделим числитель и знаменатель на НОД(51,60)=3.
, разделим числитель и знаменатель на НОД(51,60)=3.
Пример Найти разность дробей 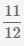 и
и 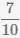 .
.
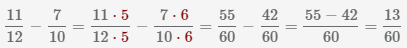
Наименьший общий знаменатель дробей равен НОК(12, 10)=60
Можно воспользуйтесь калькулятором для приведения дробей к наименьшему общему знаменателя.