Логарифмы

Логарифмы введение

Логарифмы

Логарифм отвечает на вопрос: в какую степень мы должны возвести число a чтобы получить число b.

Пример Сколько раз нужно умножить 3 чтобы получить 81?

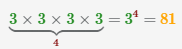
Чтобы получить число 81, нужно умножить 3 четыре раза, иначе говоря возвести число 3 в 4 степень и получить 81: логарифм 81 по основанию 3

Число 4 будет является логарифмом, можно записать также в форме 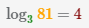логарифм 81 по основанию 3 , также говорят что 4 является логарифмом числа 81 по основанию 3.

Работаю с логарифмом мы оперируем тремя числами: основание - 3, показатель степени числа - 4, число которое хотим получить(возведя основание в степень) - 81.

Определение

Пусть a > 0, b > 0, a ≠ 1, тогда 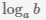логарифм b по основанию a есть такое число c, что a^c=b.

Основное логарифмическое тождество:

Пример Рассмотрим примеры вычисления логарифма с основанием 2, 4, 5.

#	Логарифм	Число в степени
1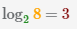
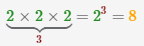2
3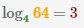
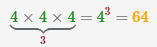4

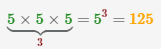Десятичные логарифмы

Логарифм по основанию 10 называют десятичным логарифмом, записывают логарифм 1000 по основанию 10

Пример Найдем десятичный логарифм чисел 100, 10000.

#	Логарифм	Число в степени
1
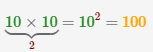2

Натуральные логарифмы

Логарифм по основанию e≈2,718 называют натуральным логарифмом, записывают натуральный логарифм

Логарифмы

Связь степени числа и логарифма

Логарифм и степень связаны, рассмотрим на примере.

Степень. Логарифм

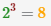2 в 3 степени показатель степени 3 говорит сколько раз нужно умножить число 2: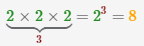

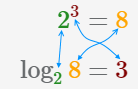Логарифм отвечает на следующий вопрос: логарифм 8 по основанию 2, записано через степень

логарифм 8 по основанию 2, записано через степень Находя логарифм, мы фактически находим показатель степени.

Отрицательные логарифмы

Пример Найти логарифмы по основанию, 2, 5, 10

#	Логарифм	Число в степени
1
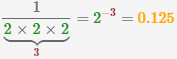2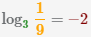
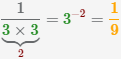3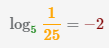

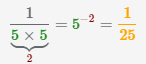Для решение примеров используйте формулы логарифмов и основные тождества.