Наибольший общий делитель. Наименьшее общее кратное.

Калькулятор поможет найти наибольший общий делитель и наименьшее общее кратное

Для вычисления введите в поля целые числа.

Нахождение наибольшего общего делителя

Нахождение НОД с помощью разложения на простые множители

Наибольшее натуральное число, на которое делятся без остатка числа a и b, называют наибольшим общим делителем этих чисел. Обозначают НОД(a, b).

Рассмотрим нахождения НОД на примере двух натуральных чисел 18 и 60:

1 Разложим числа на простые множители:
18 = 2 × 3 × 3
60 = 2 × 2 × 3 × 5
2 Вычеркнуть из разложения первого числа все множители которые не входят в разложения второго числа, получим 2 × 3 × 3.
3 Перемножаем оставшиеся простые множители после вычеркивания и получаем наибольший общий делитель чисел: НОД(18, 60)=2 × 3= 6.
4 Заметим что не важно из первого или второго числа вычеркиваем множители, результат будет одинаков:
18 = 2 × 3 × 3
60 = 2 × 2 × 3 × 5

Пример Найти наибольший общий делитель чисел 324, 111 и 432

Разложим числа на простые множители:

324 = 2 × 2 × 3 × 3 × 3 × 3

111 = 3 × 37

432 = 2 × 2 × 2 × 2 × 3 × 3 × 3

Вычеркнуть из первого числа, множители которых нету во втором и третьем числе, получим:

2 × 2 × 2 × 2 × 3 × 3 × 3 = 3

В результате НОД(324, 111, 432)=3

Нахождение НОД с помощью алгоритма Евклида

Второй способ нахождения наибольшего общего делителя с помощью алгоритма Евклида. Алгоритм Евклида является наиболее эффективным способом нахождения НОД, используя его нужно постоянно находить остаток от деления чисел и применять рекуррентную формулу.

Рекуррентная формула для НОД, НОД(a, b)=НОД(b, a mod b), где a mod b - остаток от деления a на b.

Алгоритм Евклида

Пример Найти наибольший общий делитель чисел 7920 и 594

Найдем НОД(7920, 594) с помощью алгоритма Евклида, вычислять остаток от деления будем с помощью калькулятора.

НОД(7920, 594)
НОД(594, 7920 mod 594) = НОД(594, 198)
НОД(198, 594 mod 198) = НОД(198, 0)
НОД(198, 0) = 198

7920 mod 594 = 7920 - 13 × 594 = 198
594 mod 198 = 594 - 3 × 198 = 0

В результате получаем НОД(7920, 594) = 198

Нахождение наименьшего общего кратного

Нахождение НОК с помощью разложения на простые множители

Наименьшим общим кратным натуральных чисел a и b называют наименьшее натурально число, которое кратно и a, и b. Обозначают НОК(a, b).

Рассмотрим нахождения НОК на примере двух натуральных чисел 18 и 60:

1 Разложим числа на простые множители:
18 = 2 × 3 × 3
60 = 2 × 2 × 3 × 5
2 Добавляем отсутствующие множители из разложения второго числа, получим 2 × 2 × 3 × 3 × 5.
3 Перемножаем простые множители после добавления и получаем наименьшее общее кратное чисел: НОК(18, 60)=2 × 2 × 3 × 3 × 5= 180.

Пример Найти наименьшее общее кратное чисел 168, 231 и 60

Разложим числа на простые множители:

168 = 2 × 2 × 2 × 3 × 7

231 = 3 × 7 × 11

60 = 2 × 2 × 3 × 5

Добавляем в первое число множители из второго и третьего числа, получим:

2 × 2 × 2 × 3 × 5 × 7 × 11 = 9240.

В результате НОК(168, 231, 60)=9240

Нахождение наименьшее общего кратное с помощью наибольшего общего делителя

Если известен НОД чисел, НОК можно вычислить по формуле 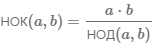$формула нахождения НОК через НОД$

Пример Найти наименьшее общее кратное чисел 54 и 72, если НОД(54, 72) = 18.

Воспользуемся формулой нахождения НОК через НОД получим:

$найдем НОК(54,72) с помощью НОД(54, 72)$

Свойства НОД и НОК

Свойства наибольшего общего делителя

НОД(a, b) = НОД(b, a)
НОД(a, b) = НОД(-a, b)
НОД(a, b) = НОД(|a|,|b|)
НОД(a, 0) = |a|
НОД(a, к • a) = |a|, при любом к ∈ Z
НОД(a, НОД(b, с)) = НОД(НОД(a, b), c)

Если d | a и d | b, то d | (a+b) и d | (a-b)
Если d | a и d | b, то d | (ax+by) для любых целых x и y

d | a - означает d делит без остатка a

Свойства наименьшего общего кратного

НОК(a, b) = НОК(b, a)
НОД(a, b) = НОД(-a, b)
НОД(a, b) = НОД(|a|,|b|)
НОК(a, НОК(b, с)) = НОК(НОК(a, b), c)

Отношение НОК и НОД: $формула нахождения НОК через НОД$